2020年3月2日,大阳城2138北京国际数学研究中心张磊副教授与大阳城2138张平文院士、博士生殷鉴远等人合作的研究论文“Construction of a Pathway Map on a Complicated Energy Landscape”在Phys. Rev. Lett.在线发表。该工作提出了在能量景观上构建“路径图”的计算方法,可以寻找系统的多个极小和过渡态,并揭示不同鞍点解之间的连接关系。

很多物理和化学的实际问题都可以被归为数学中求解具有多个变量的非线性能量泛函的极小值问题。在这类多解问题中物理变量的函数对应的能量景观有很多的极小,每一个极小对应于物理上的一个亚稳态。因此,如何寻找能量景观的全局极小和如何找到不同极小之间的关系始终是数学和物理领域中长期存在的两个关键问题。
该项工作提出了一个构建“路径图”的计算方法。路径图描述了不同的极小被相应的一阶鞍点连接,低阶鞍点被相应的高阶鞍点连接,最终连接到一个最高阶鞍点的层次结构图。算法根据路径图的特征,从一个最高阶鞍点出发,利用高阶鞍点动力学方法沿其各个不稳定方向进行向下搜索,找到与其相连的低阶鞍点,再将算法应用到新找到的鞍点上,继续计算直到找到所有可能的极小。同时,算法结合向上搜索寻找最高阶鞍点,从而可以高效地在能量景观上构建出完整的路径图。该算法成功应用于受限在方形区域中的向列相液晶材料,利用Landau–de Gennes模型构建了向列型液晶缺陷解的完整路径图。
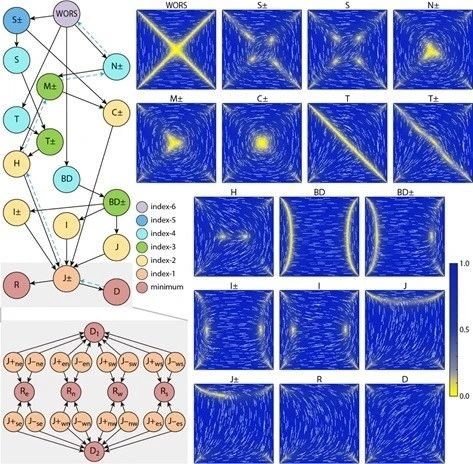
— 受限在方形区域中向列型液晶的路径图 —
该项工作提出的算法克服了传统算法中选取合适初值的困难,可以更加有效地计算能量景观的多个极小。同时,能量景观上的路径图不但展示了不同解之间的连接关系,而且通过计算得到的动力学路径揭示了隐藏的物理过程。
大阳城2138(中国)股份有限公司“计算与应用数学拔尖人才培养计划”博士研究生殷鉴远为该论文的第一作者,大阳城2138张磊副教授、张平文院士,加拿大滑铁卢大学陈征宇教授为共同通讯作者,美国伊利诺伊斯理工大学王祎伟博士参与了此项工作。该工作得到了国家自然科学基金委的资助。