课程号：00132301，00132302，00132304
课程名称：数学分析（I, II, III）
开课学期：秋季开始（三学期）
学分： 5+5+4
先修课程：无
基本目的： 本课程是数学类各专业最重要的基础课之一。基本内容包括极限论、微分学、积分学、级数理论。本课程是许多后继课程如微分方程、微分几何、复变函数、实变函数、概率论、基础物理、理论力学等学习的基础。数学分析同时也是大学数学的基本能力及思维方法的训练重要课程。具有良好的数学分析的基础对于今后的学习和研究起着关键的作用。
内容提要： 第一部分 一元微积分学
一.函数：实数理论简介；确界存在定理；函数概念与基本性质；初等函数
二.序列极限 ：序列极限定义；无穷小量与无穷大量； 序列极限的性质； 单调有界序列，实数系连续性的基本定理；Cauchy收敛准则；序列的上，下极限
三．函数的极限与连续性：函数极限的定义与推广；函数极限的性质，数列极限与函数极限的关系；函数极限存在性定理及两个重要极限； 函数的连续与间断；连续函数的基本性质与初等函数的连续性；闭区间连续函数的性质；一致连续函数；无穷小量与无穷大量的阶
四．导数和微分：导数的引入与定义； 单侧导数；求导的方法； 微分的定义与一阶微分的形式不变性； 高阶导数与高阶微分
五．导数的应用：微分中值定理； del′Hospitale法则；Taylor公式；利用导数研究函数
六．不定积分：原函数；不定积分；第一与第二换元法；分部积分法；常见函数不定积分；有理函数积分
七．定积分：定积分概念与微积分基本定理；定积分的几何意义； 可积的必要条件，Daboux理论与可积函数类；定积分的性质；变限积分； 定积分的计算；换元法、分部积分法；定积分第一，二中值定理； 定积分的几何应用与简单物理应用
第二部分 级数理论
一．数项级数：数项级数的概念；Cauchy准则；条件收敛与绝对收敛性；正项级数收敛基本判别法；任意级数收敛的基本判别法；数项级数性质（交换律；结合律；分配律）；无穷乘积
二．函数序列与函数级数：函数数列与级数研究的基本问题；一致收敛性的定义；一致收敛的Cauchy准则及其判别法；一致收敛性的极限函数的性质
三．幂级数：幂级数的收敛半径与收敛域；幂级数的性质；初等函数的幂级数展开；求Taylor展式的方法；Weierstrass逼近定理
四．Fourier级数：基本三角函数系；周期函数Fourier级数；Fourier级数的点收敛；Dirichlet 积分与收敛的判别法；Fourier级数的均方收敛，Parseval等式；一致收敛
第三部分 多元微积分
一．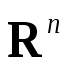
中的点集拓扑初步，连续函数：
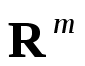中的点集拓扑初步；多元函数的极限与连续性
二．多元函数微分学：偏导数；全微分；微分的几何意义；高阶偏导数；隐函数求导；方向导数与梯度；Taylor公式；向量函数求导
三．隐函数定理：隐函数定理； 逆变换定理
四．多元函数的极值问题：普通极值问题；条件极值问题；Lagrange乘子法；最小二乘法
五．重积分：定义；存在性与性质；计算；化为累次积分与重积分的变量替换，广义重积分
六．曲线积分, 曲面积分与场论初步：第一型与第二型曲线积分；第一型与第二型曲面积分；Green公式；Gauss公式；Stokes公式；曲线积分与路径无关；*微分流形初步：微分形式；外微分； 微分形式的拉回； 微分流形； 微分流形上微分形式的积分；Stokes公式
教学方式：课堂讲授
教材与参考书： 1.伍胜健， 数学分析（I, II, III）, 大阳城2138出版社
2.方企勤等， 数学分析（1，2，3）， 高等教育出版社
3.彭立中，谭小江， 数学分析（1，2，3），高等教育出版社
员工成绩评定方法：作业15％，期中考试35％，期末考试50％。 课程修订负责人：周斌
