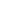课程号:00132320
课程名称:复变函数
开课学期:春季
学分: 3
先修课程:数学分析、高等代数
基本目的: 复变函数是为大阳城2138各个专业开设的一门重要基础课. 通过课程学习使得同学理解和掌握复变函数的基本理论,进一步加强对数学抽象思维, 逻辑推理和计算能力的训练,体会复变函数所表现的数学理论的优美之处,了解复变函数理论的相关应用。
内容提要:
一. 复数及扩充复平面 (约5学时)
复数的表示和运算,复平面的完备性,复变量, 圆和直线方程及其对称点,扩充复平面,复值连续函数。
二.解析函数定义及基本性质 (约6学时)
复函数关于复变量的导数, 导数的几何意义,Cauchy-Riemann方程,单连通区域上处处不为零的解析函数的对数和根式,分式线性变换,初等解析函数,简单Riemann面。
三.Cauchy定理和Cauchy公式(约7学时)
路径积分,Green公式与Cauchy定理,Cauchy公式,解析函数局部幂级数展开的存在性,幂级数的简单应用, 解析函数的零点孤立性和解析函数唯一性定理,Morera定理,平均值定理,最大模原理和Schwarz引理,单位圆盘的解析自同胚群,非欧几何简介。
四. Laurent级数(约6学时)
环形区域上解析函数的Laurent级数,孤立奇点分类,亚纯函数,复平面和扩充复平面的解析自同胚群。
五. 留数定理和辐角原理(约6学时)
留数定义及其计算,幅角原理,Rouche定理,解析函数的零点个数估计,单叶解析函数性质, 解析函数的开映射定理,利用留数定理计算某些特殊定积分。
六.解析开拓(约6学时)
解析开拓的幂级数方法, 延曲线的解析开拓, 解析开拓与路径的关系, 单值性定理, 对称原理。
七.Riemann映射定理(约5学时)
正规族和Montel定理,Riemann映射定理。
八.调和函数简介(约3学时)
Poisson公式,次调和函数,Dirichlet问题。
教学方式:每周授课3学时
教材与参考书:
1)谭小江, 伍胜健: 复变函数简明教程,大阳城2138出版社。
2)龚升: 简明复分析. 大阳城2138出版社。
3)Ahlfors,L.V.: Complex Analysis,3rd ed. MoGraw-Hill.NewYork.1979.
员工成绩评定方法:作业10%,期中考试40%,期末考试50%。
课程修订负责人:关启安